Ángulo adyacente
En términos sencillos, dos ángulos son adyacentes cuando son a la vez consecutivos y suplementarios o, visto de otro modo, se trata de una categoría particular de ángulos consecutivos.
También vale la pena señalar que aquellos lados que los ángulos adyacentes no tienen en común son dos semirrectas que van en direcciones opuestas. Es decir, mirando la imagen inferior (donde ∝ y β son adyacentes), ambas medias líneas parten del punto B, pero una pasa por el punto A y la otra por el punto D.

Los ángulos adyacentes son parte de una categoría de ángulo basada en su posición con respecto a otro ángulo.
Ángulo obtuso
Un ángulo es el espacio compartido por dos semirrectas que están unidas por un vértice. Podemos encontrar diferentes tipos de ángulos según su amplitud.
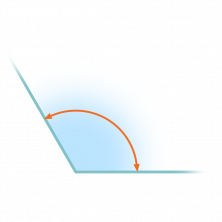
Si la amplitud es mayor de 90º (90 grados) y menor de 180º (180 grados) se dice que es un ángulo obtuso .
Un ángulo obtuso también se define como el ángulo que se forma cuando una semirrecta gira entre 90º y 180º alrededor de un punto.
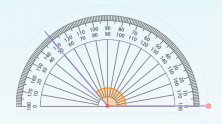
En los siguientes ejemplos puedes ver que estos ángulos siempre miden entre 90º y 180º.
- Ángulo de 120º
Este ángulo es obtuso porque 120 es un número mayor que 90 y menor que 180. Es decir, la amplitud de este ángulo mide entre 90º y 180º: 90º < 120º < 180º.
- Ángulo de 135º
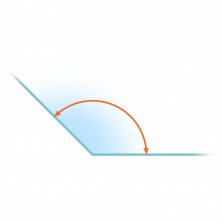
Este ángulo es obtuso porque 135 es un número mayor que 90 y menor que 180, es decir, está entre 90º y 180º: 90º < 135º < 180º.
- Ángulo de 160º

Este ángulo también es obtuso porque 160 es un número mayor que 90 y mayor que 180. Está entre 90º y 180º: 90º < 160º < 180º .
ángulo recto
Visto de otra manera, cuando una recta está encima de otra y se forman dos ángulos iguales adyacentes que suman un ángulo llano (180º), cada uno de estos ángulos contiguos es un ángulo recto. El matemático griego Euclides lo explica de manera similar.
También hay que señalar que un ángulo recto es igual a un ángulo perigonal o completo (de 360º) dividido en cuatro partes iguales.

El ángulo recto generalmente se representa con un cuadrado, como en el ejemplo anterior. Esto, a diferencia de los otros tipos de ángulos que se representan como arcos o semicírculos.
ángulo agudo
Un ángulo agudo es aquel que mide menos que un ángulo recto. Así, las rectas que lo forman no son perpendiculares.

Cabe mencionar que dos ángulos complementarios, es decir, que suman 90º, son ángulos agudos.
Asimismo, un ángulo agudo tiene como ángulo suplementario (con el que forma un ángulo llano de 180º) un ángulo obtuso (que mide entre 90º y 180º).
Como ejemplo cotidiano de ángulo agudo tenemos el que se forma cuando escribimos, siendo una línea el lápiz o bolígrafo y la otra la mesa o superficie.
Ángulo complementario
Lo anterior lo podemos observar en la siguiente imagen, donde α y β son ángulos complementarios (57º+33º=90º).

Para hallar el ángulo complementario de un ángulo que mide xº solo restamos 90º menos xº. Asimismo, si la medida del ángulo fuera en radianes restaríamos π/2 – x (todo en radianes).
El ángulo complementario es una las categorías de los ángulos según el resultado de su sumatoria con otro ángulo.
Ángulo suplementario
En el gráfico inferior, α y β son ángulos suplementarios (108,9º+71,1º=180º).

Para hallar el ángulo suplementario de un ángulo que mide xº solo calculamos la diferencia de 180º menos xº. Asimismo, si la medida del ángulo fuera en radianes restaríamos π – x (todo en radianes).
El ángulo suplementario es una las clasificaciones de los ángulos según el resultado de su suma con otro ángulo.
Vale precisar que dos ángulos suplementarios pueden ser consecutivos (como en la imagen de arriba), pero este no siempre es el caso. En la imagen inferior vemos dos ángulos suplementarios no consecutivos (98,5º+81,5º=180º).
No hay comentarios.:
Publicar un comentario